CppNoddy: include/ODE_BVP.h File Reference

A specification of a class for an 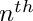$n^{th}$ -order ODE BVP defined by. More...

#include <DenseVector.h>
#include <DenseMatrix.h>
#include <Equation_1matrix.h>
#include <OneD_Node_Mesh.h>
#include <Uncopyable.h>
#include <Residual.h>
#include <Timer.h>
#include <ArcLength_base.h>
#include <BandedLinearSystem.h>
#include <Utility.h>
#include <LinearEigenSystem_base.h>
#include <DenseLinearEigenSystem.h>

Go to the source code of this file.

Classes
class	CppNoddy::ODE_BVP< _Type, _Xtype >
	A templated object for real/complex vector system of first-order ordinary differential equations. More...

Namespaces
namespace	CppNoddy
	A collection of OO numerical routines aimed at simple (typical) applied problems in continuum mechanics.

Detailed Description

A specification of a class for an 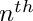$n^{th}$ -order ODE BVP defined by.

${\underline f}^\prime (y) = {\underline R}( {\underline f}(y), y )\,,$

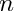
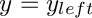
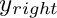
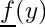
subject to Dirichlet conditions defined at $y = y_{left}$ or $y_{right}$ for some components of ${\underline f}(y)$ . The system is solved by applying Newton iteration, with the intermediate problem:

${\underline g}^\prime (y) - \frac{\partial {\underline R}}{\partial \underline f} \Big \vert_{\underline F} \,\,{\underline g}(y) = {\underline R}( {\underline F}(y), y) - {\underline F}^\prime (y) \,,$

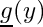
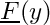
for the corrections $\underline g(y)$ to the current approximation to the solution ${\underline F}(y)$ . The numerical scheme can be run for any given distribution of nodes and can adapt the nodal positions based on residual evaluations (including both refinement and unrefinement).

Definition in file ODE_BVP.h.

Classes

Namespaces

Detailed Description