CppNoddy: include/PDE_IBVP.h File Reference

A specification of a class for an 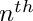$n^{th}$ -order IBVP of the form. More...

#include <DenseVector.h>
#include <DenseMatrix.h>
#include <Equation_2matrix.h>
#include <Residual_with_coords.h>
#include <OneD_Node_Mesh.h>
#include <Uncopyable.h>
#include <Timer.h>

Go to the source code of this file.

Classes
class	CppNoddy::PDE_IBVP< _Type >
	A templated object for real/complex vector system of unsteady equations. More...

Namespaces
namespace	CppNoddy
	A collection of OO numerical routines aimed at simple (typical) applied problems in continuum mechanics.

Detailed Description

A specification of a class for an 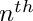$n^{th}$ -order IBVP of the form.

$M_1( {\underline f}(y,t), y, t )\cdot {\underline f}_t (y,t)+ M_0( {\underline f}(y,t), y, t ) \cdot {\underline f}_y (y,t) = {\underline R}( {\underline f}(y,t), y, t )\,,$

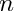
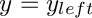
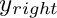
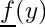
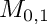
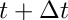
subject to conditions defined at $y = y_{left}$ and $y_{right}$ for some components of ${\underline f}(y)$ . Here $M_{0,1}$ are matrices. The solution at the new time step $t+\Delta t$ is

${\underline f}^{new} = {\underline F} + {\underline g}$

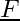
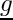
where ${\underline F}$ is the current guess at the solution and ${\underline g}$ is the linearised correction. The solution at the previous time is

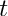
${\underline f}^{old} = {\underline O}$

A Crank-Nicolson method is employed with the linearised problem at the mid-time point $t + \Delta t /2$ being:

$\frac{2}{\Delta t} M_1 \cdot {\underline g } + 2 M_0 \cdot {\underline g}_y - J \cdot {\underline g} + J_2 \cdot \frac{\underline F - \underline O}{\Delta t} \cdot {\underline g} + J_1 \cdot \frac{\underline F_y + \underline O_y}{2} \cdot {\underline g} = 2 {\underline R} - \frac{2}{\Delta t} M_2 \cdot ( {\underline F} - {\underline O} ) - M_1 \cdot ( {\underline F}_y + {\underline O}_y )$

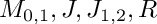
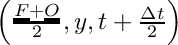
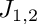
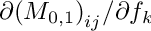
Where $M_{0,1}, J, J_{1,2}, R$ are evaluated at the mid-time step with arguments $\left ( \frac{\underline F + \underline O}{2}, y, t + \frac{\Delta t}{2} \right )$ , with $J_{1,2}$ denoting the Jacobian of the matrices $\partial {(M_{0,1})}_{ij} / \partial f_k$ . This problem is solved by second-order central differencing at the spatial ( ) inter-node mid points.

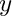
Definition in file PDE_IBVP.h.

Classes

Namespaces

Detailed Description