Solving the Blasius equation. More...
Go to the source code of this file.
Classes | |
| class | CppNoddy::Example::Blasius_equation |
| Define the Blasius equation by inheriting Equation base class. More... | |
| class | CppNoddy::Example::Blasius_left_BC |
| class | CppNoddy::Example::Blasius_right_BC |
Namespaces | |
| namespace | CppNoddy |
| A collection of OO numerical routines aimed at simple (typical) applied problems in continuum mechanics. | |
| namespace | CppNoddy::Example |
Enumerations | |
| enum | { f , fd , fdd } |
Functions | |
| int | main () |
Detailed Description
Solving the Blasius equation.
![\[ f'''(y) + f(y) f''(y) = 0\,, \]](form_83.png)
with 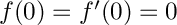
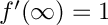
![$ y \in [0,\infty ] $](form_87.png)
Definition in file BVPBlasius.cpp.
Enumeration Type Documentation
◆ anonymous enum
| anonymous enum |
Function Documentation
◆ main()
| int main | ( | ) |
Definition at line 77 of file BVPBlasius.cpp.
78{
79 cout << "\n";
80 cout << "=== BVP: finite-difference solution of Blasius ======\n";
81 cout << "\n";
82
83 cout << " Number of points : approx. error \n";
84
85 // equation
86 Example::Blasius_equation problem;
87 // boundary conditions
88 Example::Blasius_left_BC BC_left;
89 Example::Blasius_right_BC BC_right;
90
91 double left = 0.0; // from x=0
92 double right = 20.0; // to x=20
94
95 const double tol = 1.e-5; // pass/fail tolerance
96 // let's repeat the computation for a sequence of N's
97 // to check on convergence
98 for ( int N = 32; N <= 2048; N *= 2 )
99 {
100 // mesh
102 // pass it to the ode
103 ODE_BVP<double> ode( &problem, nodes, &BC_left, &BC_right );
104 for ( int i = 0; i < N; ++i )
105 {
106 double y = ode.solution().coord( i );
107 ode.solution()( i, f ) = y * ( 1.0 - exp( -y ) );
108 ode.solution()( i, fd ) = ( 1.0 - exp( -y ) ) + y * exp( -y );
109 ode.solution()( i, fdd ) = 2.0 * exp( -y ) - y * exp( -y );
110 }
111
112 try
113 {
114 ode.solve2();
115 }
116 catch ( const std::runtime_error &error )
117 {
118 cout << " \033[1;31;48m * FAILED THROUGH EXCEPTION BEING RAISED \033[0m\n";
119 return 1;
120 }
121
122 const double c = 1.65519036023e0;
123 const double answer = 1. / pow( c, 1.5 );
125 {
127 }
128 else
129 {
131 }
132
133 // compare to the known stress value
134 std::cout << " N=" << N << " error=" << abs( ode.solution()( 0, fdd ) - answer ) << " IVP answer=" << answer << "\n";
135
136 std::string dirname("./DATA");
137 mkdir( dirname.c_str(), S_IRWXU );
138 ode.solution().dump_gnu("./DATA/blasius.data");
139
140 }
141
142 if ( failed )
143 {
144 cout << "\033[1;31;48m * FAILED \033[0m\n";
145 return 1;
146 }
147 else
148 {
149 cout << "\033[1;32;48m * PASSED \033[0m\n";
150 return 0;
151 }
152}
A templated object for real/complex vector system of first-order ordinary differential equations.
Definition: ODE_BVP.h:37
DenseVector< double > power_node_vector(const double &lower, const double &upper, const std::size_t &N, const double &power)
Return a DENSE vector with the nodal points of a non-uniform mesh distributed between the upper/lower...
Definition: Utility.cpp:123
References f, fd, fdd, CppNoddy::Utility::power_node_vector(), CppNoddy::ODE_BVP< _Type, _Xtype >::solution(), and CppNoddy::ODE_BVP< _Type, _Xtype >::solve2().
 1.9.5
1.9.5