BVPKarmanAdaptive.cpp File Reference

Adaptively solve the Karman rotating-disk equations for the flow above an infinite rotating disk: More...

#include <BVP_bundle.h>
#include "../Utils_Fill.h"

Go to the source code of this file.

Classes
class	CppNoddy::Example::Karman_equations
	Define the Karman equations. More...
class	CppNoddy::Example::Karman_left_BC
	Define the boundary conditions. More...
class	CppNoddy::Example::Karman_right_BC

Namespaces
namespace	CppNoddy
	A collection of OO numerical routines aimed at simple (typical) applied problems in continuum mechanics.
namespace	CppNoddy::Example

Enumerations
enum	{   U , Ud , V , W ,   Wd }

Functions
int	main ()

Detailed Description

Adaptively solve the Karman rotating-disk equations for the flow above an infinite rotating disk:

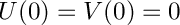
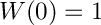
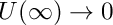
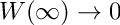
with boundary conditions , and , . The class constructs and solves the global matrix problem using 2nd-order finite differences.

Definition in file BVPKarmanAdaptive.cpp.

Enumeration Type Documentation

anonymous enum

anonymous enum

Enumerator
U
Ud
V
W
Wd

Definition at line 19 of file BVPKarmanAdaptive.cpp.

{U, Ud, V, W, Wd};

Function Documentation

main()

int main

(

)

Definition at line 84 of file BVPKarmanAdaptive.cpp.

{
  cout << "\n";
  cout << "=== BVP: finite-difference soln of Karman eqns ======\n";
  cout << "===  Here we use an adaptive mesh after timing.   ===\n";
  cout << "\n";
 
  Example::Karman_equations problem;
  Example::Karman_left_BC BC_left;
  Example::Karman_right_BC BC_right;
 
  // Boundary layer is from 0 to 20
  double left = 0.0;
  double right = 40.0;
  // number of nodal points
  int N = 21;
 
  DenseVector<double> nodes = Utility::power_node_vector( left, right, N, 1.5 );
 
  ODE_BVP<double> ode( &problem, nodes, &BC_left, &BC_right );
 
  for ( int i = 0; i < N; ++i )
  {
    double y = ode.solution().coord( i );
    ode.solution()( i, U ) = 0.0;
    ode.solution()( i, Ud ) = 0.0;
    ode.solution()( i, V ) = 0.0;
    ode.solution()( i, W ) = exp( -y );
    ode.solution()( i, Wd ) = -exp( -y );
  }
 
  try
  {
    ode.solve2();
  }
  catch (const std::runtime_error &error )
  {
    cout << " \033[1;31;48m  * FAILED THROUGH EXCEPTION BEING RAISED \033[0m\n";
    return 1;
  }
  std::cout << "===  Adapting the mesh.\n";
 
  // output to check the adapted mesh
  std::string dirname("./DATA");
  mkdir( dirname.c_str(), S_IRWXU );
  TrackerFile my_file( "./DATA/BVP_Karman.dat", 12 );
  my_file.push_ptr( &ode.solution(), "soln" );
 
  const double tol( 1.e-4 );
  int adapt_counter ( 1 );
  do
  {
    // one adapt
    ode.adapt( 1.e-4 );
    ++adapt_counter;
    // solve
    ode.solve2();
    // no. of nodes in the adapted mesh
    N = ode.solution().get_nnodes();
    cout << " Adapted mesh to " << ode.solution().get_nnodes() << " nodes.\n";
    cout << " Adapted error = " << abs( ode.solution()( N - 1, V ) + 0.88447 ) << "\n";
    // adapt until condition is satisfied or max adaptions are done
  }
  while ( ( abs( ode.solution()( N - 1, V ) + 0.88447 ) > tol ) && ( adapt_counter < 10 ) );
  // store solution for plotting
  my_file.update();
 
  // check the BL transpiration vs the known solution
  if ( abs( ode.solution()( N - 1, V ) + 0.88447 ) > tol )
  {
    cout << "\033[1;31;48m  * FAILED \033[0m\n";
    cout << " Difference = " << abs( ode.solution()( N - 1, V ) + 0.88447 ) << "\n";
    return 1;
  }
  else
  {
    cout << "\033[1;32;48m  * PASSED \033[0m\n";
    return 0;
  }
 
}

References CppNoddy::ODE_BVP< _Type, _Xtype >::adapt(), CppNoddy::Utility::power_node_vector(), CppNoddy::TrackerFile::push_ptr(), CppNoddy::ODE_BVP< _Type, _Xtype >::solution(), CppNoddy::ODE_BVP< _Type, _Xtype >::solve2(), U, Ud, CppNoddy::TrackerFile::update(), V, W, and Wd.