Solving the equation. More...
#include <BVP_bundle.h>Go to the source code of this file.
Classes | |
| class | CppNoddy::Example::Nonidentity_equation< _Type, _Xtype > |
| Define the harmonic equation by inheriting the Equation base class. More... | |
| class | CppNoddy::Example::Nonidentity_left_BC< _Type > |
| class | CppNoddy::Example::Nonidentity_right_BC< _Type > |
Namespaces | |
| namespace | CppNoddy |
| A collection of OO numerical routines aimed at simple (typical) applied problems in continuum mechanics. | |
| namespace | CppNoddy::Example |
Enumerations | |
| enum | { f , fd } |
Functions | |
| int | main () |
Detailed Description
Solving the equation.
![\[ f(y) f''(y) + f'(y)^2 = 1+\gamma y \]](form_102.png)
subject to 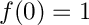
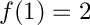
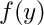
![\[ f(y)=\left ( y^2 + \frac{\gamma}{3}y^3 + (2-\frac{\gamma}{3}) y + 1 \right )^{1/2}\,.\]](form_106.png)
Definition in file BVPNonIdentityMatrix0.cpp.
Enumeration Type Documentation
◆ anonymous enum
| anonymous enum |
Function Documentation
◆ main()
| int main | ( | ) |
Definition at line 80 of file BVPNonIdentityMatrix0.cpp.
81{
82 cout << "\n";
83 cout << "=== BVP: finite-difference, non-identity matrix0 ====\n";
84 cout << "\n";
85
86 Example::Nonidentity_equation<double, double> problem;
87 Example::Nonidentity_left_BC <double> BC_left;
88 Example::Nonidentity_right_BC<double> BC_right;
89
90 double left = 0.0;
91 double right = 1.0;
92 // number of nodal points
93 unsigned N = 151;
94 // a real mesh -- along real axis
96 // Example tolerance
97 const double tol = 1.e-4;
98
99 // a real ODE BVP
100 problem.gamma = 5.0;
101 ODE_BVP<double> ode( &problem, nodes, &BC_left, &BC_right );
102
103 // our initial guess
104 for ( unsigned i = 0; i < N; ++i )
105 {
106 double y = ode.solution().coord( i );
107 // set f(y)
108 ode.solution()( i, f ) = 1+y;
109 // set f'(y)
110 ode.solution()( i, fd ) = 1;
111 }
112
113 // solve the problem using 2nd order finite-difference
114 try
115 {
116 ode.solve2();
117 }
118 catch (const std::runtime_error& error )
119 {
120 cout << " \033[1;31;48m * FAILED THROUGH EXCEPTION BEING RAISED \033[0m\n";
121 return 1;
122 }
123
124
125 // find deviation from exact solution
126 double diff = 0;
127 for ( unsigned i = 0; i < N; ++i )
128 {
129 const double y( ode.solution().coord(i) );
130 const double exact( sqrt(y*y + problem.gamma*y*y*y/3 + (2-problem.gamma/3)*y + 1) );
131 diff = std::max( std::abs( ode.solution().get_interpolated_vars(y)[f] - exact ), diff );
132 }
133
134 // validation test
135 if ( diff > tol )
136 {
137 cout << "\033[1;31;48m * FAILED \033[0m\n";
138 cout << "Real problem error " << diff << "\n";
139 return 1;
140 }
141 else
142 {
143 cout << "\033[1;32;48m * PASSED \033[0m\n";
144 return 0;
145 }
146}
A templated object for real/complex vector system of first-order ordinary differential equations.
Definition: ODE_BVP.h:37
DenseVector< double > uniform_node_vector(const double &lower, const double &upper, const std::size_t &N)
Return a DENSE vector with the nodal points of a uniform mesh distributed between the upper/lower bou...
Definition: Utility.cpp:113
References f, fd, CppNoddy::Example::Nonidentity_equation< _Type, _Xtype >::gamma, CppNoddy::ODE_BVP< _Type, _Xtype >::solution(), CppNoddy::ODE_BVP< _Type, _Xtype >::solve2(), and CppNoddy::Utility::uniform_node_vector().
 1.9.5
1.9.5