EVPComplex_lapack.cpp File Reference

Solves a 4x4 complex generalised eigenvalue problem. More...

#include <EVP_bundle.h>

Go to the source code of this file.

Functions
int	main ()

Detailed Description

Solves a 4x4 complex generalised eigenvalue problem.

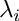
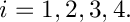
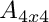
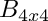
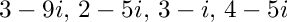
for the 4 eigenvalues , . In this case and are such that the eigenvalues are . The computation requests eigenvalues that satisfy , which in this case is .

Definition in file EVPComplex_lapack.cpp.

Function Documentation

main()

int main

(

)

Definition at line 17 of file EVPComplex_lapack.cpp.

{
  cout << "\n";
  cout << "=== EVP: complex generalised eigenvalue problem  ====\n";
  cout << "\n";
 
  DenseMatrix<D_complex> a( 4, 4, 0.0 );
 
  a( 0, 0 ) = D_complex( -21.10, -22.50 );
  a( 0, 1 ) = D_complex( 53.50, -50.50 );
  a( 0, 2 ) = D_complex( -34.50, 127.50 );
  a( 0, 3 ) = D_complex( 7.50, 0.50 );
 
  a( 1, 0 ) = D_complex( -0.46, -7.78 );
  a( 1, 1 ) = D_complex( -3.50, -37.50 );
  a( 1, 2 ) = D_complex( -15.50, 58.50 );
  a( 1, 3 ) = D_complex( -10.50, -1.50 );
 
  a( 2, 0 ) = D_complex( 4.30, -5.50 );
  a( 2, 1 ) = D_complex( 39.70, -17.10 );
  a( 2, 2 ) = D_complex( -68.50, 12.50 );
  a( 2, 3 ) = D_complex( -7.50, -3.50 );
 
  a( 3, 0 ) = D_complex( 5.50, 4.40 );
  a( 3, 1 ) = D_complex( 14.40, 43.30 );
  a( 3, 2 ) = D_complex( -32.50, -46.00 );
  a( 3, 3 ) = D_complex( -19.00, -32.50 );
 
  DenseMatrix<D_complex> b( 4, 4, 0.0 );
 
  b( 0, 0 ) = D_complex( 1.00, -5.00 );
  b( 0, 1 ) = D_complex( 1.60, 1.20 );
  b( 0, 2 ) = D_complex( -3.00, 0.00 );
  b( 0, 3 ) = D_complex( 0.00, -1.00 );
 
  b( 1, 0 ) = D_complex( 0.80, -0.60 );
  b( 1, 1 ) = D_complex( 3.00, -5.00 );
  b( 1, 2 ) = D_complex( -4.00, 3.00 );
  b( 1, 3 ) = D_complex( -2.40, -3.20 );
 
  b( 2, 0 ) = D_complex( 1.00, 0.00 );
  b( 2, 1 ) = D_complex( 2.40, 1.80 );
  b( 2, 2 ) = D_complex( -4.00, -5.00 );
  b( 2, 3 ) = D_complex( 0.00, -3.00 );
 
  b( 3, 0 ) = D_complex( 0.00, 1.00 );
  b( 3, 1 ) = D_complex( -1.80, 2.40 );
  b( 3, 2 ) = D_complex( 0.00, -4.00 );
  b( 3, 3 ) = D_complex( 4.00, -5.00 );
 
  // a vector for the eigenvalues
  DenseVector<D_complex> lambdas;
  // eigenvalues are: (3,-9), (2,-5), (3,-1), (4,-5)
 
  DenseLinearEigenSystem<D_complex> system( &a, &b );
  try
  {
    system.eigensolve();
  }
  catch (const std::runtime_error &error )
  {
    cout << " \033[1;31;48m  * FAILED THROUGH EXCEPTION BEING RAISED \033[0m\n";
    return 1;
  }
 
  // tag any eigenvalues within a distance of 0.1 of the point 3-i
  system.set_shift( D_complex( 3.0, -1.0 ) );
  system.tag_eigenvalues_disc( + 1, 0.1 );
  // get those tagged eigenvalues
  lambdas = system.get_tagged_eigenvalues();
  const double tol = 1.e-14;
  if ( std::abs( lambdas[ 0 ] - D_complex( 3.0, -1.0 ) ) > tol )
  {
    cout << "\033[1;31;48m  * FAILED \033[0m\n";
    cout.precision( 12 );
    cout << "    Final error = " << std::abs( lambdas[ 0 ] - D_complex( 3.0, -1.0 ) ) << "\n";
    lambdas.dump();
    return 1;
  }
 
  cout << "\033[1;32;48m  * PASSED \033[0m\n";
  return 0;
 
}

References CppNoddy::DenseVector< _Type >::dump(), CppNoddy::DenseLinearEigenSystem< _Type >::eigensolve(), CppNoddy::DenseLinearEigenSystem< _Type >::get_tagged_eigenvalues(), CppNoddy::LinearEigenSystem_base::set_shift(), and CppNoddy::DenseLinearEigenSystem< _Type >::tag_eigenvalues_disc().