EVPHarmonicLocal.cpp File Reference

Solves the harmonic equation. More...

#include <BVP_bundle.h>
#include "../Utils_Fill.h"

Go to the source code of this file.

Classes
class	CppNoddy::Example::Harmonic_equation< _Type, _Xtype >
	Define the harmonic equation by inheriting the Equation base class. More...
class	CppNoddy::Example::Harmonic_left_BC< _Type >
class	CppNoddy::Example::Harmonic_right_BC< _Type >

Namespaces
namespace	CppNoddy
	A collection of OO numerical routines aimed at simple (typical) applied problems in continuum mechanics.
namespace	CppNoddy::Example

Enumerations
enum	{ f , fd , lambda }

Functions
int	main ()

Detailed Description

Solves the harmonic equation.

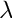
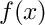
as a LOCAL eigenvalue problem for over the unit domain with homogeneous boundary conditions for but using the nonlinear BVP solver to refine a guess at an eigenvalue. For example, we would have run an (expensive) global eigenvalue search (EVP_Harmonic) then refined the eigenvalue of interest in the way shown in this example.

Note: This approach (as it stands) is not as efficient as it could be since we include N extra degrees of freedom (where N is the number of mesh points) into the problem for only one eigenvalue. This retains the banded structure, but it would perhaps be better to solve using a sparse structure, or an appropriate multi-step algorithm for the for the banded matrix.

Definition in file EVPHarmonicLocal.cpp.

Enumeration Type Documentation

anonymous enum

anonymous enum

Enumerator
f
fd
lambda

Definition at line 25 of file EVPHarmonicLocal.cpp.

{ f, fd, lambda };

Function Documentation

main()

int main

(

)

Definition at line 88 of file EVPHarmonicLocal.cpp.

{
  cout << "\n";
  cout << "=== EVP: Local refinement of an eigenvalue  =========\n";
  cout << "\n";
 
  cout << " Number of points : |local eigenvalue - pi^2| \n";
 
  // set up the problem
  Example::Harmonic_equation problem;
  // set up BCs
  Example::Harmonic_left_BC BC_left;
  Example::Harmonic_right_BC BC_right;
  // set up the domain from 0 to 1
  double left = 0.0;
  double right = 1.0;
  // set our guess for the eigenvalue -- this would come
  // from the global method in a less trivial problem.
  D_complex eigenvalue_guess = 9.0;
  bool failed( true );
  // loop through some meshes with increasing numbers of points
  for ( unsigned i = 6; i <= 10; ++i )
  {
    unsigned N( 0 );
    N = unsigned( std::pow( 2.0, double( i ) ) );
    // mesh
    DenseVector<double> nodes( Utility::uniform_node_vector( left, right, N ) );
    // construct the ODE_BVP object
    ODE_BVP<D_complex> ode( &problem, nodes, &BC_left, &BC_right );
    // makes no sense to monitor the determinant here
    ode.set_monitor_det( false );
    // run through the mesh & set an initial guess
    for ( unsigned i = 0; i < N; ++i )
    {
      double x = ode.solution().coord( i );
      ode.solution()( i, f ) = x * ( 1 - x );
      ode.solution()( i, fd ) = 1.0 - 2 * x;
      ode.solution()( i, lambda ) = eigenvalue_guess;
    }
    // solve for the eigenvalue/eigenfunction
    ode.solve2();
    // an error measure
    double abs_error( std::abs( ode.solution()( 1, lambda ) - M_PI * M_PI ) );
    // output for fun
    cout << "  " << N << " : " << abs_error << "\n";
    if ( abs_error < 1.e-4 )
      failed = false;
  }
 
  if ( failed )
  {
    cout << "\033[1;31;48m  * FAILED \033[0m\n";
    return 1;
  }
 
  cout << "\033[1;32;48m  * PASSED \033[0m\n";
  return 0;
}

References f, fd, lambda, CppNoddy::ODE_BVP< _Type, _Xtype >::set_monitor_det(), CppNoddy::ODE_BVP< _Type, _Xtype >::solution(), CppNoddy::ODE_BVP< _Type, _Xtype >::solve2(), and CppNoddy::Utility::uniform_node_vector().