28{
29 SlepcSession::getInstance(argc,argv);
30
31 cout << "\n";
32 cout << "=== EVP: Harmonic equation solved using SLEPc ======\n";
33 cout << "=== with a manually assembled matrix problem.\n";
34 cout << "\n";
35
36 cout.precision( 12 );
37 cout << " Number of nodal points : Leading eigenvalue error : Total CPU time taken (ms) \n";
39 size_t N = 4;
40
43 for ( int i = 2; i < 11; ++i )
44 {
45 N = ( size_t ) ( std::pow( 2., i ) );
46 const double delta = 1. / ( N - 1 );
48
49 typedef double PETSC_type;
51
52
56
57 a( 0, 0 ) = 1.0;
58 a( 0, 1 ) = 0.0;
59 a( N - 1, N - 1 ) = 1.0;
60 a( N - 1, N - 2 ) = 0.0;
61
62
65 b.scale( -1.0 );
66 b( 0, 0 ) = 0.0;
67 b( N - 1, N - 1 ) = 0.0;
68
70
71 SparseLinearEigenSystem<PETSC_type> system( &a, &b );
72 system.set_calc_eigenvectors( true );
73 system.set_nev(4);
74 system.set_order( "EPS_TARGET_MAGNITUDE" );
75
77 try
78 {
79 system.eigensolve();
80 }
81 catch (const std::runtime_error &error )
82 {
83 cout << " \033[1;31;48m * FAILED THROUGH EXCEPTION BEING RAISED \033[0m\n";
84 return 1;
85 }
86 system.tag_eigenvalues_disc( + 1, 10. );
87 lambdas = system.get_tagged_eigenvalues();
88 eigenvectors = system.get_tagged_eigenvectors();
89 cout << " " << N << " : " << lambdas[ 0 ].real() - M_PI * M_PI
90 <<
" : " << timer.
get_time() <<
"\n";
92 }
93
94
95 const double tol = 1.e-4;
96 if ( abs( lambdas[ 0 ].
real() - M_PI * M_PI ) > tol )
98
99 if ( failed )
100 {
101 cout << "\033[1;31;48m * FAILED \033[0m\n";
102 cout <<
" Final error = " << abs( lambdas[ 0 ].
real() - M_PI * M_PI ) <<
"\n";
103 return 1;
104 }
105
106 cout << "\033[1;32;48m * PASSED \033[0m\n";
107 return 0;
108}
A matrix class that constructs a DENSE matrix as a row major std::vector of DenseVectors.
An DenseVector class – a dense vector object.
A matrix class that constructs a SPARSE matrix as a row major std::vector of SparseVectors.
A simple CPU-clock-tick timer for timing metods.
double get_time() const
Return the time.
void start()
Start the timer & reset stored time to zero.
void stop()
Stop the clock & add the current time interval to the previously stored values ready for printing.
DenseVector< double > real(const DenseVector< D_complex > &X)
Return a double DENSE vector containing the real part of a complex DENSE vector.
void fill_identity(CppNoddy::Sequential_Matrix_base< _Type > &A)
Fill diagonal with unit values.
void fill_band(CppNoddy::Sequential_Matrix_base< _Type > &A, const int &offset, const _Type &value)
Fill a diagonal band of a matrix.
![\[ f''(x) + \lambda f(x) = 0 \]](form_132.png)
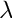
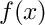
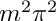
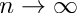
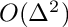
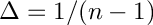
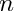
![\[ f''(x_i) + \lambda f(x_i) = \frac{ f_{i-1} - 2f_i + f_{i+1} }{ \Delta^2 } + \lambda f_i + O(\Delta^2) \]](form_139.png)
 1.9.5
1.9.5