25{
26 SlepcSession::getInstance(argc,argv);
27
28 cout << "\n";
29 cout << "=== EVP: Temporal spectra of the Orr-Sommerfeld eqn =\n";
30 cout << "=== with a matrix problem assembled by hand and \n";
31 cout << "=== eigenproblem solved with SLEPc sparse solver.\n";
32 cout << "\n";
33
34
35 const std::size_t nodes( 1001 );
36
37 const std::size_t N( 2 * nodes );
38
39 const double left = -1.0;
40 const double right = 1.0;
41
42 const double d = ( right - left ) / ( nodes - 1 );
43
44
47
48
49 const double alpha ( 1.02 );
50 const double Re ( 5772.2 );
52
53
54 a( 0, 0 ) = 1.0;
55 a( 1, 0 ) = -1.5 / d;
56 a( 1, 2 ) = 2.0 / d;
57 a( 1, 4 ) = -0.5 / d;
58
59 for ( std::size_t i = 1; i <= nodes - 2; ++i )
60 {
61
62 const double y = left + i * d;
63
64 const double U = ( 1.0 - y * y );
65 const double Udd = -2.0;
66
67
68 std::size_t row = 2 * i;
69 a( row, row ) = -2.0 / ( d * d ) - alpha * alpha;
70 a( row, row - 2 ) = 1.0 / ( d * d );
71 a( row, row + 2 ) = 1.0 / ( d * d );
72 a( row, row + 1 ) = -1.0;
73
74 row += 1;
75
76 a( row, row ) = -2.0 / ( d * d ) - alpha * alpha - I * alpha * Re *
U;
77 a( row, row - 2 ) = 1.0 / ( d * d );
78 a( row, row + 2 ) = 1.0 / ( d * d );
80
81 b( row, row ) = - I *
alpha *
Re;
82 }
83
84 a( N - 2, N - 2 ) = 1.5 / d;
85 a( N - 2, N - 4 ) = -2.0 / d;
86 a( N - 2, N - 6 ) = 0.5 / d;
87 a( N - 1, N - 2 ) = 1.0;
88
89
90
91
92
93
95 SparseLinearEigenSystem<D_complex> system( &a, &b );
97 system.set_nev(4);
98 system.set_order( "EPS_TARGET_MAGNITUDE" );
99
100 try
101 {
102 system.eigensolve();
103 }
104 catch (const std::runtime_error &error )
105 {
106 cout << " \033[1;31;48m * FAILED THROUGH EXCEPTION BEING RAISED \033[0m\n";
107 return 1;
108 }
109
110 system.set_shift(
D_complex( 0.0, -0.1 ) );
111 system.tag_eigenvalues_upper( + 1 );
112 lambdas = system.get_tagged_eigenvalues();
114 double min_growth_rate( lambdas[ 0 ].
imag() );
115
116 const double tol = 1.e-3;
117
118 std::string dirname("./DATA");
119 mkdir( dirname.c_str(), S_IRWXU );
120
122 spectrum.push_ptr( &lambdas, "evs" );
123 spectrum.update();
124
125
127 eigenvectors = system.get_tagged_eigenvectors();
130
131 if ( lambdas.
nelts() > 0 ) {
132 int index(0);
133 for ( unsigned i = 0; i < nodes; ++i ) {
134 mesh(i,0) = eigenvectors(index,2*i+0);
135 mesh(i,1) = eigenvectors(index,2*i+1);
136 }
137 for ( unsigned i = 1; i < nodes-1; ++i ) {
138 mesh(i,2) = (mesh(i+1,0)-mesh(i-1,0))/(2*d);
139 mesh(i,3) = -I*
alpha*mesh(i,0);
140 }
141 }
142 mesh.normalise(0);
143 mesh.dump_gnu("./DATA/eigenmode.dat");
144
145 if ( std::abs( min_growth_rate ) < tol )
146 {
147 cout << "\033[1;32;48m * PASSED \033[0m\n";
148 return 0;
149 }
150
151 cout << "\033[1;31;48m * FAILED \033[0m\n";
152 cout << " Final error = " << min_growth_rate << "\n";
153 return 1;
154
155}
A matrix class that constructs a DENSE matrix as a row major std::vector of DenseVectors.
An DenseVector class – a dense vector object.
std::size_t nelts() const
Get the number of elements in the vector Since the vector is dense, the number of elements is the siz...
void dump() const
Dump to std::cout.
A one dimensional mesh utility object.
A matrix class that constructs a SPARSE matrix as a row major std::vector of SparseVectors.
double Udd(double y)
Globally define the base flow curvature.
double Re
Globally define the Reynolds number and wavenumber.
DenseVector< double > imag(const DenseVector< D_complex > &X)
Return a double DENSE vector containing the imaginary part of a complex DENSE vector.
DenseVector< double > uniform_node_vector(const double &lower, const double &upper, const std::size_t &N)
Return a DENSE vector with the nodal points of a uniform mesh distributed between the upper/lower bou...
std::complex< double > D_complex
A complex double precision number using std::complex.
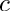
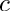
![\[ \phi''(y) - \alpha^2 \phi(y) - \psi(y) = 0\,, \]](form_142.png)
![\[ \psi''(y) - \alpha^2 \psi(y) - i \alpha Re \left \{ ( U(y) - c ) \psi(y) - U''(y) \phi \right \} = 0\,, \]](form_143.png)
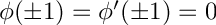
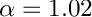
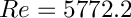
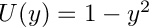
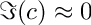
 1.9.5
1.9.5