Solves the Rayleigh problem for values 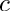
Go to the source code of this file.
Namespaces | |
| namespace | CppNoddy |
| A collection of OO numerical routines aimed at simple (typical) applied problems in continuum mechanics. | |
| namespace | CppNoddy::Example |
Functions | |
| D_complex | CppNoddy::Example::U (const D_complex &y) |
| D_complex | CppNoddy::Example::Udd (const D_complex &y) |
| int | main () |
Variables | |
| OneD_Node_Mesh< D_complex, D_complex > | CppNoddy::Example::baseflow |
Detailed Description
Solves the Rayleigh problem for values 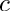
![\[ (U_B(y)-c) (\phi''(y) - \alpha^2 \phi(y)) - U_B''(y) \phi(y) = 0\,, \]](form_152.png)
subject to 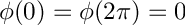
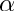
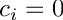
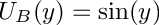
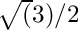
Definition in file EVPRayleigh_lapack.cpp.
Function Documentation
◆ main()
| int main | ( | ) |
Definition at line 38 of file EVPRayleigh_lapack.cpp.
39{
40
41 cout << "\n";
42 cout << "=== EVP: Rayleigh modes, Tollmien's example =========\n";
43 cout << "\n";
44
45 Example::alpha = 0.8; // the wavenumber
46 double tol = 1.e-5; // tolerance for the test
47 double left = 0.0; // from y = 0
48 double right = 2 * M_PI; // to y= 2*pi
49 unsigned N( 801 );
50 // a real distribution of nodes
52 DenseVector<D_complex> c_nodes( r_nodes );
53 // make a distribution of nodes in the complex plane
54 for ( unsigned i = 0; i < N; ++i )
55 {
56 D_complex y( r_nodes[ i ] );
57 c_nodes[ i ] -= .2 * D_complex( 0.0, 1.0 ) * y * std::exp( - y );
58 }
59
60 // make a base flow on the complex distribution of nodes
61 OneD_Node_Mesh<D_complex, D_complex> base( c_nodes, 2 );
62 for ( unsigned i = 0; i < c_nodes.size(); ++i )
63 {
64 D_complex y = c_nodes[ i ];
65 base( i, 0 ) = Example::U( y );
66 base( i, 1 ) = Example::Udd( y );
67 }
68
69 // make the Rayleigh EVP, with 'CHANNEL' boundary conditions
71 // do a global solve
72 my_ray.global_evp();
73
74 unsigned i_ev = 0;
75 for ( unsigned i = 0; i < my_ray.eigenvalues().size(); ++i )
76 {
77 if ( my_ray.eigenvalues()[ i ].imag() > 0.05 )
78 {
79 // there should be only one
80 i_ev = i;
81 }
82 }
83
84 my_ray.iterate_to_neutral( i_ev );
85
86 if ( std::abs( my_ray.alpha() - .5*sqrt( 3. ) ) < tol )
87 {
88 cout << "\033[1;32;48m * PASSED \033[0m\n";
89 return 0;
90 }
91 cout << "\033[1;31;48m * FAILED \033[0m\n";
92 cout << " Final error in critical wavenumber = " << std::abs( my_ray.alpha() - .5*sqrt( 3. ) ) << "\n";
93 return 1;
94
95}
Definition: HST.h:18
DenseVector< double > power_node_vector(const double &lower, const double &upper, const std::size_t &N, const double &power)
Return a DENSE vector with the nodal points of a non-uniform mesh distributed between the upper/lower...
Definition: Utility.cpp:123
std::complex< double > D_complex
A complex double precision number using std::complex.
Definition: Types.h:98
References CppNoddy::HST::Rayleigh< _Type >::alpha(), CppNoddy::HST::Rayleigh< _Type >::eigenvalues(), CppNoddy::HST::Rayleigh< _Type >::global_evp(), CppNoddy::HST::Rayleigh< _Type >::iterate_to_neutral(), CppNoddy::Utility::power_node_vector(), and CppNoddy::DenseVector< _Type >::size().
 1.9.5
1.9.5