EVPShootBiharmonic.cpp File Reference

Solving a one-dimensional "Bi-harmonic" eigenvalue problem (EVP) More...

#include <IVP_bundle.h>

Go to the source code of this file.

Classes
class	CppNoddy::Example::Biharmonic_equation
	Define the biharmonic eigenvalue equation by inheriting Equation base class. More...
class	CppNoddy::Example::Biharmonic_residual
	Define a residual function using the boundary conditions for the biharmonic_equation. More...

Namespaces
namespace	CppNoddy
	A collection of OO numerical routines aimed at simple (typical) applied problems in continuum mechanics.
namespace	CppNoddy::Example

Functions
int	main ()

Detailed Description

Solving a one-dimensional "Bi-harmonic" eigenvalue problem (EVP)

via Runge-Kutta and (vector) Newton iteration. The problem is nonlinear since 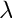is unknown.

Locally solving for eigenvalues using IVP methods is generally speaking not a great way of doing things; this is just a Example rather than any recommendation! See the other EVP examples for better methods.

Definition in file EVPShootBiharmonic.cpp.

Function Documentation

main()

int main

(

)

Definition at line 88 of file EVPShootBiharmonic.cpp.

{
 
  cout << "\n";
  cout << "=== EVP: Biharmonic equation via shooting  ==========\n";
  cout << "\n";
 
  Example::Biharmonic_residual problem;
  // instantiate a complex Vector Newton class for the Biharmonic
  Newton<D_complex> Biharm( &problem );
 
  const D_complex A( -3.0, 7.0 );        // A guess of f'''(0)
  const D_complex B( 2.21, 1.25 );       // A guess of the eigenvalue
  // rig up an initial guess
  DenseVector<D_complex> unknowns( 2, 0.0 );          // Two complex quantities to to find
  unknowns[ 0 ] = A;
  unknowns[ 1 ] = B * B;
 
  try
  {
    Biharm.iterate( unknowns );
  }
  catch (const std::runtime_error &error )
  {
    cout << " \033[1;31;48m  * FAILED THROUGH EXCEPTION BEING RAISED \033[0m\n";
    return 1;
  }
 
  D_complex eigenvalue( std::sqrt( unknowns[ 1 ] ) );
 
  std::string dirname("./DATA");
  mkdir( dirname.c_str(), S_IRWXU );
  // output for the data
  TrackerFile my_file( "./DATA/Biharmonic.dat" );
  my_file.push_ptr( &eigenvalue, "eigenvalue" );
  my_file.push_ptr( &problem.ode -> get_mesh(), "biharmonic" );
  my_file.header();
  my_file.update();
 
  const double tol = 1.e-8; // A pass/fail tolerance
  if ( abs( sin( eigenvalue ) + eigenvalue ) < tol )
  {
    cout << "\033[1;32;48m  * PASSED \033[0m\n";
    return 0;
  }
 
  cout << "\033[1;31;48m  * FAILED \033[0m\n";
  cout << "   Diff = " << abs( sin( eigenvalue ) + eigenvalue ) << "\n";
  return 1;
 
}

References CppNoddy::TrackerFile::header(), CppNoddy::Newton< _Type >::iterate(), CppNoddy::Example::Biharmonic_residual::ode, CppNoddy::TrackerFile::push_ptr(), and CppNoddy::TrackerFile::update().