HYPNonlinearAdvection.cpp File Reference

Solving the 1D ‘nonlinear advection equation’. More...

#include <OneD_HYP_bundle.h>

Go to the source code of this file.

Classes
class	CppNoddy::Example::NlinAdv
	Define the system. More...

Namespaces
namespace	CppNoddy
	A collection of OO numerical routines aimed at simple (typical) applied problems in continuum mechanics.
namespace	CppNoddy::Example

Functions
void	CppNoddy::Example::Q_init (const double &x, DenseVector< double > &q)
	Set the initial state of the system. More...
int	main ()

Detailed Description

Solving the 1D ‘nonlinear advection equation’.

using a TVD Lax-Friedrichs scheme for . The initial condition is taken to be

The test is simply conservation of 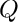in this case.

Definition in file HYPNonlinearAdvection.cpp.

Function Documentation

main()

int main

(

)

Definition at line 72 of file HYPNonlinearAdvection.cpp.

{
  cout << "\n";
  cout << "=== Hyperbolic: 1D nonlinear advection equation  ====\n";
  cout << "\n";
 
  // define the domain/mesh
  const double left =  0.0;
  const double right = 1.0;
  const unsigned N = 141;
  DenseVector<double> faces_x = Utility::uniform_node_vector( left, right, N );
 
  double t = 0.0;
 
  Example::NlinAdv conservative_problem;
  OneD_TVDLF_Mesh NlinAdv_mesh( faces_x, &conservative_problem, Example::Q_init );
  NlinAdv_mesh.set_limiter( 0 );
 
  double I1 = NlinAdv_mesh.integrate()[0];
  int loop_counter( 5 );
 
  std::string dirname("./DATA");
  mkdir( dirname.c_str(), S_IRWXU );
  TrackerFile my_file( "./DATA/HYP_NlinAdv.dat" );
  // first column of the output will always be the time
  my_file.push_ptr( &t, "time" );
  OneD_Node_Mesh<double> soln = NlinAdv_mesh.get_soln();
  my_file.push_ptr( &soln, "mesh" );
 
  double asym( 0.0 );
  do
  {
    double dt = NlinAdv_mesh.update( 0.475 );
    t += dt;
    soln = NlinAdv_mesh.get_soln();
 
    if ( loop_counter % 10 == 0 )
    {
      soln = NlinAdv_mesh.get_soln();
      my_file.update();
      my_file.newline();
    }
    ++loop_counter;
    asym = std::max( asym, std::abs( soln.get_interpolated_vars( 0.75 )[0] + soln.get_interpolated_vars( 0.25 )[0] ) );
  }
  while ( ( t < 0.4 ) && ( loop_counter < 1000 ) );
 
  double I2 = NlinAdv_mesh.integrate()[0];
  soln = NlinAdv_mesh.get_soln();
  my_file.update();
  my_file.newline();
  // problem should be antisymmetric about x = 1/2
  if ( ( asym > 1.e-10 ) || ( std::abs( I1 - I2 ) > 1.e-8 ) || ( loop_counter >= 1000 ) )
  {
    cout << "\033[1;31;48m  * FAILED \033[0m\n";
    cout << "asymmetry = " << asym << "\n";
    cout << "integral difference = " << I1 - I2 << "\n";
    cout << "loop counter = " << loop_counter << "\n";
    return 1;
  }
  else
  {
    cout << "\033[1;32;48m  * PASSED \033[0m\n";
    return 0;
  }
 
} // end of main()

References CppNoddy::OneD_Node_Mesh< _Type, _Xtype >::get_interpolated_vars(), CppNoddy::OneD_TVDLF_Mesh::get_soln(), CppNoddy::OneD_TVDLF_Mesh::integrate(), CppNoddy::TrackerFile::newline(), CppNoddy::TrackerFile::push_ptr(), CppNoddy::OneD_TVDLF_Mesh::set_limiter(), CppNoddy::Utility::uniform_node_vector(), CppNoddy::TrackerFile::update(), and CppNoddy::OneD_TVDLF_Mesh::update().