Solving the heat diffusion equation. More...
#include <IBVP_bundle.h>Go to the source code of this file.
Classes | |
| class | CppNoddy::Example::Diff_equation |
| class | CppNoddy::Example::Diff_both_BC |
Namespaces | |
| namespace | CppNoddy |
| A collection of OO numerical routines aimed at simple (typical) applied problems in continuum mechanics. | |
| namespace | CppNoddy::Example |
Enumerations | |
| enum | { f , fd } |
Functions | |
| int | main () |
Detailed Description
Solving the heat diffusion equation.
![\[ f_t = f_{yy} \]](form_201.png)
subject to 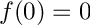
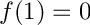
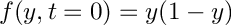
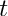

![\[ f(y,t) = \sum_{n=1,3,...}^M \frac{8}{n^3\pi^3} \sin ( n\pi y) \exp{ -n^2\pi^2 t } \]](form_204.png)
The series is truncated at the 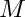
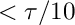
Definition in file IBVPDiffusion.cpp.
Enumeration Type Documentation
◆ anonymous enum
| anonymous enum |
| Enumerator | |
|---|---|
| f | |
| fd | |
Definition at line 19 of file IBVPDiffusion.cpp.
Function Documentation
◆ main()
| int main | ( | ) |
Definition at line 83 of file IBVPDiffusion.cpp.
References CppNoddy::PDE_IBVP< _Type >::coord(), f, fd, CppNoddy::PDE_IBVP< _Type >::solution(), CppNoddy::PDE_IBVP< _Type >::step2(), u, and CppNoddy::Utility::uniform_node_vector().
 1.9.5
1.9.5